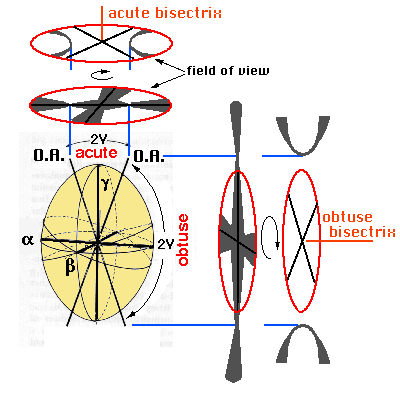
a = cut perpendicular
to the acute bisectrixThe interference
figures of biaxial crystals also vary according to the cut of the mineral
plate
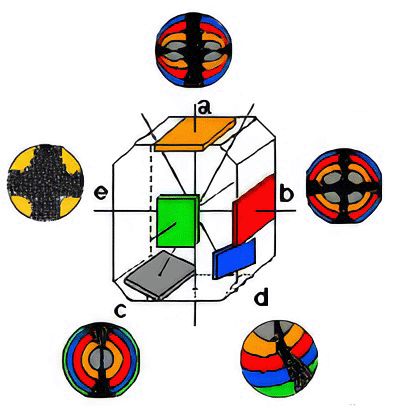
Principal orientations of the cut of the mineral plates
a = cut perpendicular
to the acute bisectrix
b = cut perpendicular to the obtuse bisectrix
c = cut perpendicular to the optic axis
d = cut inclined, general position
e = cut parallel to the plane of the optic axes
a. Cut perpendicular to the acute bisectrix
The isogyre of this cut is formed by a cross which, when the microscope stage is turned, changes into two hyperbolic curves which draw away from each other and then join again, never disappearing from the field of view altogether (movies). When the isogyres are in the form of a cross, the two bands are clearly different, one branch being broader than the other (figure 1)
. Both parts of the thinner band narrow at the points of incidence of the optic axes (known as melatopes) and these are represented in the figure 1 by the letters A and B.
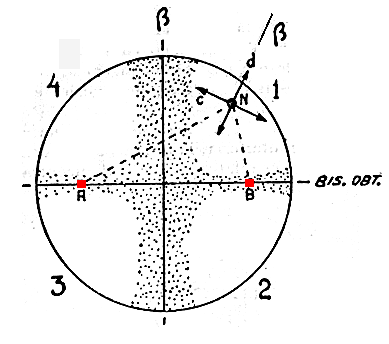
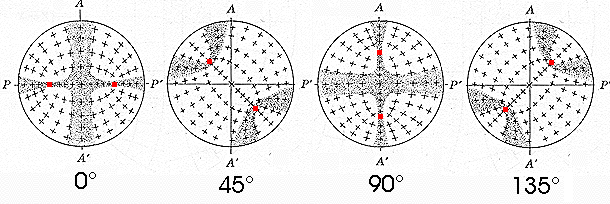
In order to establish the directions of vibration for the waves which pass through any point of the figure 1 and reconstruct the form of the isogyre, you only have to join the point in question with the melatopes: one direction of vibration is the bisecting direction (direction "d" in the figure) and the other is perpendicular to it (direction "c" in the figure).
The figure 2 shows the directions of vibration of numerous points in the optic field.
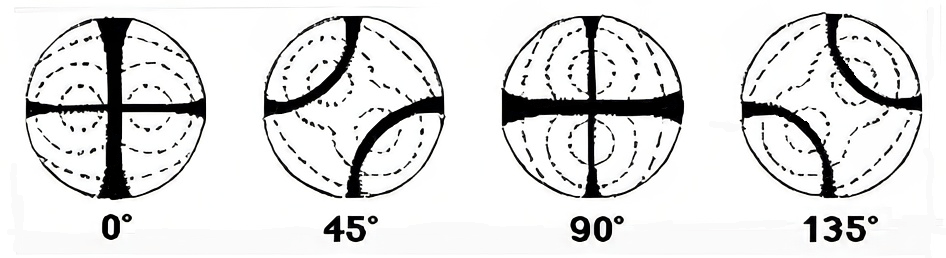
As there are two optic axes in these crystals, the isochromatic curves adopt a fairly complex configuration known as Bertin's surfaces (they form a figure-of-eight pattern), see figure 3.
b. Cut perpendicular to the obtuse bisectrix
The isogyre of this cut is formed by a cross which, when the microscope stage is turned, changes into two hyperbolic curves. The hyperbolic bands separate so much that they leave the field of view.
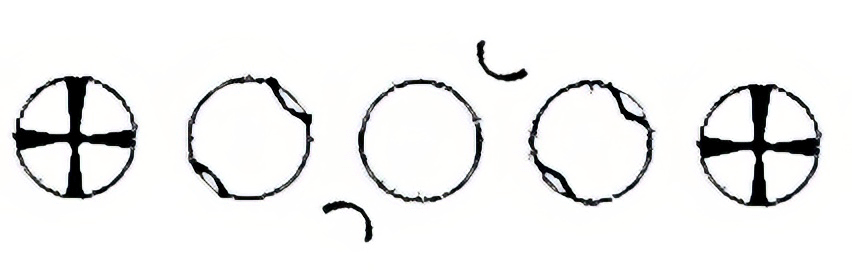
This interference figure is also presented by cuts perpendicular to the acute bisectrix when 2V is very large, and they are indistinguishable.
c = cut perpendicular to the optic axis
This is formed by a single isogyre band, situated in the centre of the field of view. It starts as a straight diameter and, as the stage is turned, it gradually bends, turning round the centre of the field and showing its concavity towards the various quadrants (it is like half the figure which appears in the cut perpendicular to the acute bisectrix).
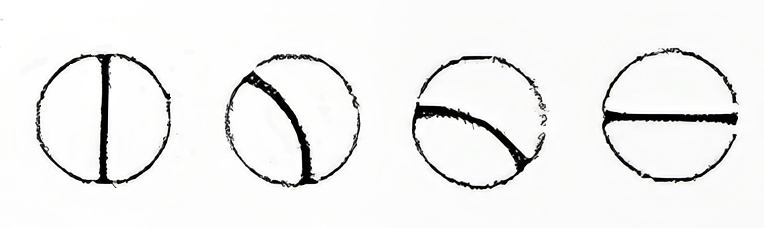
The isochromatic curves form concentric loops, in any position.
d. Cut inclined, general position
The interference figure is formed by an isogyre whose centre is situated outside the field of view. As it is turned, the figure is seen in parts. A single isogyre band is seen which moves about the field of view until it disappears altogether. Sometimes it is the vertical band of the isogyre cross that enters the field and sometimes the horizontal one does so. Sometimes it is the inclined.
The bands do not remain straight, and are bent, when leaving the field.
The figure does not distinguish uniaxial and biaxial minerals.
e. Cut parallel to the plane of the optic axes
When the cut is parallel to the plane of the optic axes (optical axes lie in to the plane of the section), a flash figure is formed, which is characterised by an isogyre cross made up of extraordinarily broad bands which occupy nearly the whole field of view. However, when the microscope stage is turned even slightly, it disappears completely.
The figure does not distinguish uniaxial and biaxial minerals.
Index | Introduction | PPL | XPL orthos | XPL conos | Previous | Next | Top