Interference colour. How is it formed? 55

Interference colour. How is it formed?

5 polariser + anisotropic mineral (general case) + analyser

5.5 Significance of retardation when using white light

In the two previous screens, we have discussed the interference of waves according to whether their retardation is equal to a wavelength or semi-wavelength. But white light is not composed of one wavelength, but of numerous radiations with different wavelengths.

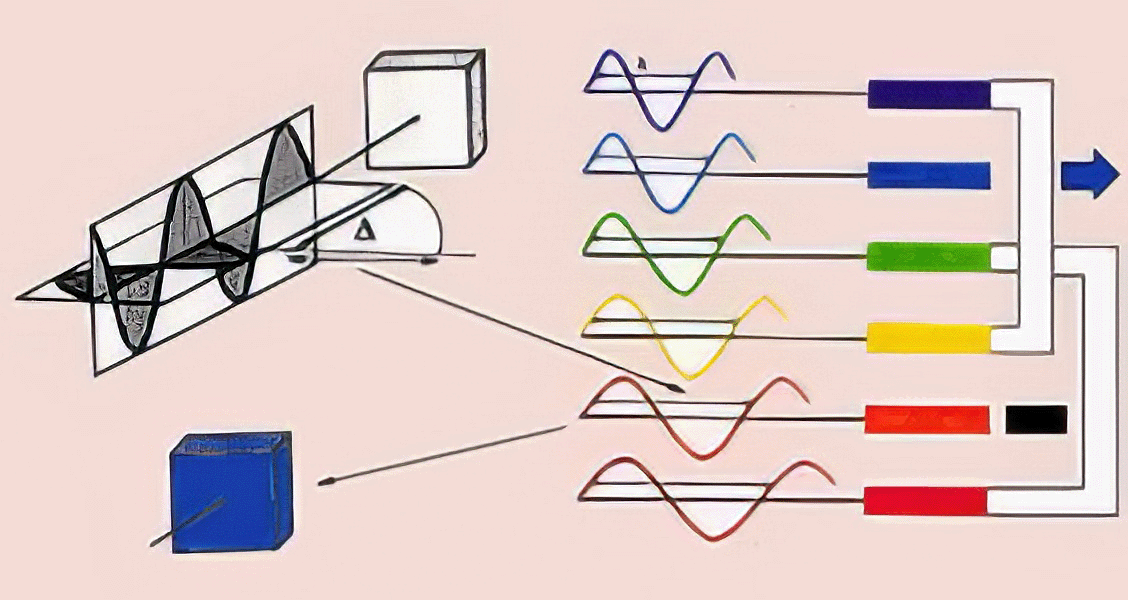
If the retardation coincides with the wavelength of some spectral colour, the corresponding radiation is annulled and, as a result, its complementary colour will appear (complementary colours have already been dealt with when considering colour),

When retardation is nil, all the colours will be annulled and the crystal will appear to be black. As retardation increases, a moment will come in which it reaches the value corresponding to the colour with the smallest wavelength: violet; the violet will be annulled and its complementary colour will appear as the interference colour: yellow. Subsequently, the retardation will reach the value of the colour with the next lowest l, which is blue; the blue will be annulled and its complementary colour, orange, will appear. This will happen successively as the wavelengths of green, yellow, orange and red are reached, and their complementary colours of interference will appear: red, violet, blue and green, respectively.

The next figure shows how as the retardation between the two waves increases, the wave-lengths of the lowest colours are reached and these colours are nullified, causing their complementary colours to appear. As the retardation increases, a grey colour will appear and a moment will come in which it reaches a value corresponding to the smallest wave-length, whose colour is violet.

In the figure 3, we can see the correspondence between the colours corresponding to the nullified and those of interference. As the effects are the same when retardation coincides with a wavelength or a multiple of it, the initial sequence repeats itself.

figure 3

What will be the effect of this?

The interference colour is the result of a phase difference between waves

In the previous screens, we have explained how the interference colour is the result of the interference, in the plane of the analyser, of the two waves which leave the crystal vibrating in perpendicular planes.

Depending on the phase difference, the interference will produce an intensification or an annulment of the waves.

The interference colour is produced when the retardation between the waves of the crystal is equal to a whole number of wavelengths corresponding to its complementary colour.

The interference colour is a characteristic of great diagnostic power in the study of minerals. It represents the birefringence of the mineral, i.e. it values the maximum difference between the refractive indices of the fast and slow waves of each mineral, and thus is a measure of its anisotropy.

Will all the grains from one mineral present the same interference colour?

NO!

The interference colour is the result of the anisotropy of the mineral. It is therefore a property which varies with direction.

Consequently, as shown in the figures, the grains show different interference colours according to how the preparation has been made (known as the cut of the mineral). The more birefringent the mineral is, the more the interference colour of its grains will vary.

What therefore will be the representative interference colour of each mineral?